Introduzione alla teoria dei grafi per la teoria dei giochi

Nell’articolo precedente (https://orbyta.it/teoria-dei-giochi/) abbiamo illustrato i principi base della teoria dei giochi e, tramite qualche esempio, abbiamo scoperto come può essere utilizzata per attuare la strategia più conveniente in una situazione in cui il guadagno finale dipende dalle mosse effettuate dagli altri giocatori.

In questo secondo articolo scopriremo cos’è la teoria dei grafi e come può essere integrata nella teoria dei giochi. Inoltre, introdurremo un altro tipo di equilibrio di Nash, ovvero gli equilibri di Nash per strategie miste.

La teoria dei grafi

I grafi possono essere utilizzati per schematizzare delle situazioni o processi e ne consentono l’analisi in termini quantitativi e algoritmici.

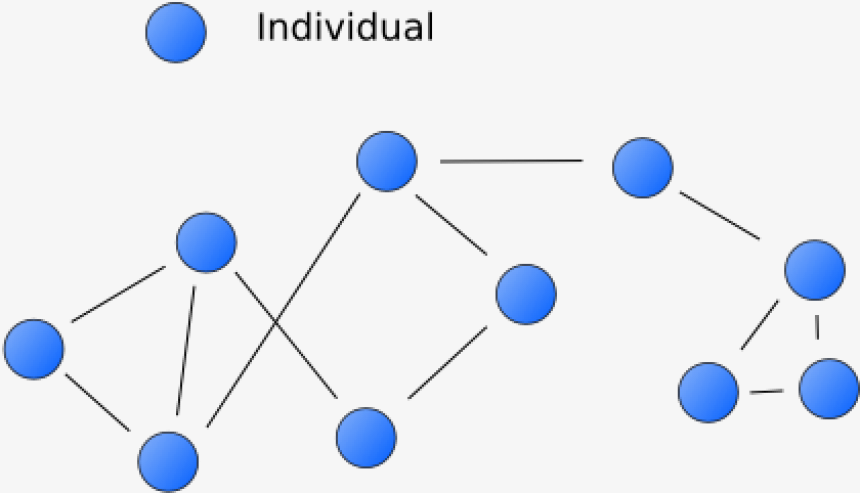
Tecnicamente, un grafo (o rete) G è una coppia (V, E) dove V è un insieme finito i cui elementi sono detti vertici o nodi ed E è un sottoinsieme i cui elementi, detti archi o lati, sono coppie di oggetti in V.

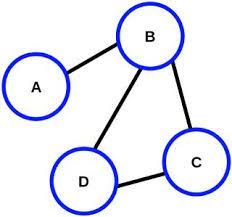
Per esempio, nella seguente immagine vediamo un grafo con vertici V={A,B,C,D} ed archi E={(A,B), (B,A), (B,D), (D,B), (D,C), (C,D), (B,C), (C,B)}.

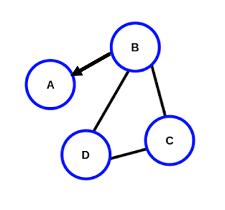
Una digrafo è un grafo che possiede almeno un arco orientato, cioè un arco caratterizzato da un verso che non può essere percorso nel verso opposto.

Per esempio modificando il grafo precedente come segue otteniamo un digrafo con archi E={(B,A), (B,D), (D,B), (D,C), (C,D), (B,C), (C,B)}.

Introduciamo ora qualche esempio pratico per capire come i grafi possono essere utilizzati nella teoria dei giochi.

Esempio numerico [4]

Consideriamo una situazione in cui sono presenti due giocatori e il primo di essi, A, sceglie un numero tra 1,2 e 3. Il secondo partecipante, B, somma al numero detto 1,2 o 3. A farà lo stesso nel turno successivo e così via finché uno dei due arriverà ad esclamare 31 vincendo.
Tale gioco può essere rappresentato tramite il seguente digrafo:

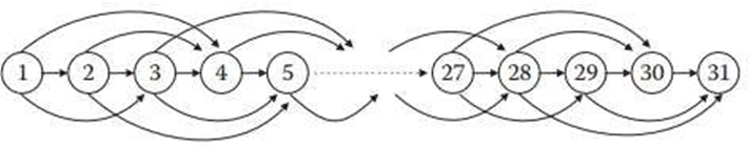
I vertici sono i numeri naturali dall’1 al 31 e gli archi che partono dal vertice n entrano in quelli n+1, n+2 e n+3 se 1 ≤ n ≤ 28. Dal 29 escono degli archi entranti in 30 e 31, dal 30 in 31 e dal 31 nessuno.

Dunque, il giocatore che riesce a dire 27 ha vinto perché il giocatore successivo potrà selezionare solo i vertici 28, 29, o 30 e, in ognuno di questi casi, il primo riuscirà a posizionarsi sul 31.

Possiamo quindi porci come obiettivo di arrivare al 27 e non al 31. Ma a questo punto chi dirà 23 riuscirà a vincere e, applicando il ragionamento iterativamente, concludiamo che i nodi da toccare per vincere sono X = {3, 7, 11, 15, 19, 23, 27, 31}.

Osserviamo che:

• Se un giocatore dice un numero non appartenente a X allora l’avversario ha sempre la possibilità di farlo e dunque di vincere.
• Se un giocatore dice un numero appartenente a X allora l’avversario non potrà che scegliere un numero ad esso non appartenente.

In conclusione, analizzando il grafo, scopriamo che l’obiettivo è quello di occupare sempre le posizioni di X.

Esempio della protesta

Supponiamo di voler manifestare contro una data azione di un governo dittatoriale. Tale evento risulterà vantaggioso solo se il numero di manifestanti sarà sufficientemente elevato, d’altro canto se ciò non dovesse accadere andremmo in contro ad un payoff assai negativo in quanto potremmo supporre che, in tal caso, lo stato sederà la manifestazione in modo violento.

Supponiamo che ogni persona decida di partecipare alla protesta solo se sa che almeno un numero sufficiente di cittadini vi aderirà.

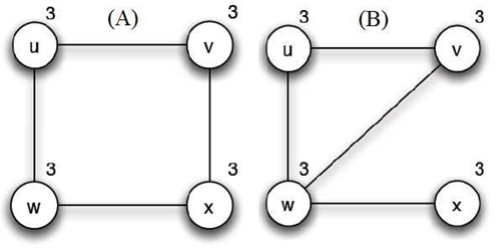
Supponiamo di avere 4 cittadini e rappresentiamo il fatto che il cittadino w conosca il comportamento di quello u e viceversa con la presenza del lato (w,u). La cifra accanto a un nodo indica il numero minimo di manifestanti totali affinché il nodo in questione si unisca all’impresa.

Consideriamo le seguenti situazioni:

Notiamo che nel caso A la rivolta non avrà luogo in quanto ognuno dei partecipanti non ha modo di sapere il comportamento che adotterà il nodo ad esso non collegato.

Nel caso B invece ognuno tra u, v e w saprà che esistono almeno altri due nodi che richiedono almeno tre partecipanti totali e che a loro volta hanno questa informazione. Dunque la protesta si svolgerà, in particolare u, v e w saranno i manifestanti.

Equilibrio di Nash per strategie miste

Esistono dei giochi in cui non sono presenti gli equilibri di Nash che abbiamo introdotto nell’articolo precedente, ovvero quelli basati su strategia pure. Una strategia pura infatti fornisce una descrizione completa del modo in cui un individuo gioca una partita. In particolare, essa determina quale scelta farà il giocatore in qualsiasi situazione che potrebbe affrontare.

Una strategia mista per un giocatore è una distribuzione di probabilità sull’insieme delle strategie pure che ha a disposizione. Ogni strategia pura P può essere vista come un caso particolare di strategia mista che assegna probabilità pari a 1 a P e pari a 0 a tutte le altre strategie pure.

Abbiamo quindi due tipi di equilibri di Nash: quelli per le strategie pure, analizzati finora, si hanno quando tutti i giocatori hanno a disposizione solo strategie pure, altrimenti si parla di equilibri di Nash per strategie miste.

Limitandoci ad un gioco a due partecipanti, un equilibrio di Nash per le strategie miste è una coppia di scelte (che ora sono probabilità) tale che ognuna sia la miglior risposta all’altra.

Introduciamo un esempio.

Esempio dell’attaccante/difensore

Si consideri un gioco in cui c’è un attaccante A e un difensore D.

L’attaccante può scegliere tra le strategie di attacco a₁ o a₂ mentre il difensore può difendersi da a₁, e quindi applicare la strategia d₁, o viceversa difendersi da a₂, e quindi applicare la strategia d₂.

Supponiamo che:

• se D scegliesse la giusta strategia di difesa, cioè d_i contro a_i (i = 1, 2), avremmo per A un guadagno di 0;
• se D scegliesse d₁ e A scegliesse a₂, A otterrebbe un guadagno di 5 e D una perdita pari;
• se D scegliesse d₂ mentre A scegliesse a₁, A ricaverebbe un guadagno di 10 e D una perdita pari.

Riassumiamo la situazione del gioco nella seguente tabella indicando in ogni riquadro: a sinistra della virgola il guadagno ottenuto da A e a destra della virgola quello ottenuto da D.

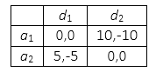
Nel nostro esempio a₁ e a₂ sono le strategie pure a disposizione dell’attaccante, mentre difendere da a₁ e difendere da a₂ quelle del difensore.

Dato che i due giocatori otterrebbero dei guadagni nettamente contrastanti potremmo concludere che in questo genere di giochi (detti strettamente competitivi) non esistano equilibri di Nash.

Se uno dei due giocatori sapesse il comportamento dell’altro allora potrebbe scegliere la strategia atta a massimizzare il suo profitto e inevitabilmente a minimizzare quello dell’avversario. Ognuno dei giocatori cercherà perciò di rendere imprevedibile la propria strategia.

Sia p la probabilità che A scelga a₁ e q la probabilità che D scelga d₁. Per ora sappiamo solo che esiste almeno un equilibrio per le strategie miste ma non quali debbano essere i valori effettivi di p e q.

Usiamo il principio secondo cui un equilibrio misto sorge quando le probabilità utilizzate da ciascun giocatore fanno sì che il suo avversario non abbia motivo di preferire una delle due opzioni disponibili all’altra.

Se supponiamo che D abbia una probabilità q di giocare d₁ allora abbiamo che i possibili guadagni per A sono:

• (0)(q) + (10)(1 − q) = 10 − 10q se scegliesse a_1;
•  (5)(q) + (0)(1 − q) = 5q se scegliesse a₂.

Per far in modo che per A sia indifferente scegliere tra a₁ e a₂ imponiamo 10−10q = 5q da cui q = 2/3.

Ora supponiamo che A abbia una probabilità p di mettere in atto a₁. I possibili guadagni per D allora sono:

• (0)(p) + (−5)(1 − p) = 5p − 5 se scegliesse d₁
• (−10)(p) + (0)(1 − p) = −10p se scegliesse d₂

Imponendo 5p − 5 = −10p otteniamo p = 1/3.

Quindi abbiamo che gli unici possibili valori di probabilità che possono apparire nell’equilibrio per la strategia mista sono p = 1/3 per l’attaccante e q = 2/3 per il difensore.

Si noti inoltre che il guadagno atteso di A nel caso in cui scelga a₁ e D scelga d₁ è di 10/3 e quello di D è di -10/3.

Ciò ci suggerisce un’analisi controintuitiva: la probabilità di A di sferrare l’attacco più forte è di un terzo, ovvero, in un modello continuo, potremmo immaginare che solo per un terzo del tempo A provi ad attaccare con a₁.

Perché usare così poco la strategia più potente?

La risposta è che se A provasse sempre ad attaccare con a₁ allora D sarebbe persuaso a rispondere spesso con d_1, il che ridurrebbe il payoff atteso da A. D’altro canto si consideri che poiché p = 1/3 fa sì che D scelga senza preferenza una delle due strategie e abbiamo che, quando A usa tale valore di probabilità, allora, indipendentemente dalle scelte di D, esso si assicura un payoff di 10/3.

Esempio delle imprese

Consideriamo ora il fatto che anche se un giocatore non ha una strategia dominante, esso potrebbe avere strategie che sono dominate da altre. Si consideri il seguente esempio.

Supponiamo che due imprese, F1 e F2, stiano progettando di aprire un negozio in una delle sei città situate lungo sei uscite consecutive su una strada. Possiamo rappresentare la disposizione di queste città utilizzando un grafo a sei nodi come quello nella figura sottostante [2].

Supponiamo che F1 possa aprire il suo negozio in A, C o E mentre F2 in B, D o F. Una volta che i negozi apriranno, i clienti delle varie città faranno compere nel centro a loro più vicino. Si assuma che ogni città abbia lo stesso numero di clienti e che i guadagni dei negozi siano direttamente proporzionali al numero di clienti attirati. Otteniamo facilmente la tabella di guadagni sottostante.

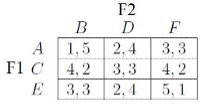
Si può verificare che nessuno dei giocatori ha una strategia dominante: per esempio se F1 scegliesse la locazione A allora la risposta strettamente migliore di F2 sarebbe B, mentre se F1 scegliesse E la risposta strettamente migliore di F2 sarebbe D. Nonostante ciò notiamo che A è una strategia strettamente dominata per F1, infatti in ogni situazione in cui F1 ha l’opzione di scegliere A, esso riceverà un guadagno strettamente migliore scegliendo C. Analogamente F è una strategia strettamente dominata per F2. Abbiamo dunque che F1 non sceglierà A e F2 non sceglierà F. Possiamo a questo punto non considerare i nodi F e A, e da ciò ricaviamo la seguente tabella di payoff:

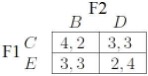
B ed E divengono rispettivamente le nuove strategie strettamente dominate per F2 e F1 e quindi possono essere a loro volta eliminate. Arriviamo alla conclusione che F1 sceglierà C e F2 D.

Questo modo di procedere è chiamato cancellazione iterativa delle strategie strettamente dominate. Notiamo inoltre che la coppia (C,D) costituisce l’unico equilibrio di Nash del gioco ed infatti questa metodologia di studio è anche utile a trovare gli equilibri di Nash. Generalizziamo di seguito il processo appena presentato.

Dato un numero arbitrario di n giocatori abbiamo che la cancellazione iterativa delle strategie strettamente dominate procede come segue:

1. Si parte da un giocatore, si trovano tutte le sue strategie strettamente dominate e le si eliminano;
2. Si considera il gioco semplificato ottenuto. Si eliminano eventuali nuove strategie strettamente dominate;
3. Si itera il processo finché non si trovano più strategie strettamente dominate.

Si può dimostrare che l’insieme degli equilibri di Nash della versione originale del gioco coincide con quello della versione finale così ottenuta.

Consideriamo un problema in cui due giocatori A e B possano optare per la strategia a o b con i seguenti guadagni simmetrici:

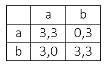
In questo caso a è una strategia debolmente dominata poiché in ogni caso ogni giocatore può solo migliorare il suo guadagno scegliendo b. Inoltre si noti che (b,b) è un equilibrio di Nash.

Quando abbiamo delle strategie debolmente dominate non è consigliabile procedere con il metodo della cancellazione, poiché questa operazione potrebbe distruggere degli equilibri.

D’altro canto è intuitivo pensare che nessun giocatore scelga di assecondare l’equilibrio (a,a) composto da strategie debolmente dominate se non ha modo di prevedere il comportamento dell’altro giocatore: perché non usare la strategia (b,b) che nel peggiore dei casi comunque non inficia il  guadagno?

In questo articolo abbiamo visto come la teoria dei grafi può essere usata in quella dei giochi andando a risolvere giochi che hanno dato risultati controintuitivi. Nel prossimo articolo, approfondiremo le reti andando a studiare situazioni più complesse che ci permetteranno di analizzare la propagazione delle strategie all’interno di una rete.

Bibliografia e sitografia

[2] D. Easley e J. Kleinberg, Networks, Crowds, and Markets: Reasoning about a Highly Con- nected World, Cambridge University Press, 2010.

[3] R. Gibbons, Teoria dei giochi, Bologna, Il Mulino, 2005.

[4] E. Martìn Novo e A. Mendez Alonso, Aplicaciones de la teoría de grafos a algunos juegos de estrategia, numero 64 di Suma, Universidad Politécnica de Madrid, 2004.

[8] P. Serafini, Teoria dei Grafi e dei Giochi, a.a. 2014-15 (revisione: 28 novembre 2014).

[9] I. S. Stievano e M. Biey, Cascading behavior in networks, DET, Politecnico di Torino, 2015.

[10] I. S. Stievano e M. Biey, Interactions within a network, DET, Politecnico di Torino, 2015.

[11] I. S. Stievano, M. Biey e F. Corinto, Reti e sistemi complessi, DET, Politecnico di Torino, 2015.

[12] A. Ziggioto e A. Piana, Modello di Lotka-Volterra, reperibile all’indirizzo http://www.itismajo.it/matematica/Lezioni/Vecchi%20Documenti%20a.s.%202011-12/Modello

%20di%20Lotka-Volterra.pdf, consultato il 15/05/2015.

 [15] http://web.econ.unito.it/vannoni/docs/thgiochi.pdf consultato il 14/05/2015.

Articolo a cura di Monica Mura e Carla Melia, Data Scientist in Orbyta Tech, 01.05.2021